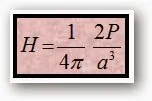المجالات المغناطيسية للتيار الكهربى

المجالات المغناطيسية للتيار الكهربى

Magnetic Fields of Electric Current

المجالات المغناطيسية للتيار الكهربى

ملاحظة / هنالك روابط لتحميل كتب فيزياء مهمة في نهاية الموضوع 

 مقدمة

من المعروف أن الخاصية المغناطيسية اكتشفت في مدينة مغنيسيا في آسيا الصغرى حيث اكتشفت أجسام تجذب إليها قطع الحديد ، سميت هذه الخاصية بالخاصية المغناطيسية وسمى هذا المغناطيس بالمغناطيس الدائم.

 وهذه الظاهرة عبارة عن قوى تجاذب أو تنافر تنشأ بين قطع من الحديد وأيضا اكتشف العلماء أن الأرض تمثل مغناطيس كبير له قطبان بدليل انه عند تعليق مغناطيس حديدي تعليقا حرا فانه يأخذ وضعا خاص بحيث يشير إلى الشمال والجنوب للأرض ولذلك استغل العلماء هذه الفكرة لصناعة البوصلة التي أصبحت وقتها الدليل لمعرفة الاتجاهات الأصلية.

معلومات خاصة بالمغناطيس الدائم:

  1ـ له قطبان شمالي وجنوبي

  2ـ الأقطاب المتشابه تتنافر والمختلفة تتجاذب بقوة تبعا لقانون نيوتن وهو يشبه قانون كولوم

  3ـ يحيط بالمغناطيس منطقة تسمى بالمجال المغناطيسي وتحتوي على خطوط المجال المغناطيسي

  4ـ المجال المغناطيسي نوعان      

 5ـ شدة المجال المغناطيسي (H) لها علاقة بكثافة الفيض المغناطيسي (B) والعلاقة هي:

A/m →    B = μ_o.H

حيث μ_o    نفاذية الفراغ أو الهواء

المجال المغناطيسي  H(Magnetic Field):

هو المنطقة التي تحيط بالمغناطيس ويظهر فيها تأثيره المغناطيسي .

وهنا سوف نتعرف على كثافة الفيض المغناطيسي (الحث المغناطيسي) (B) Magnetic Induction
والذي يتخذ كدلالة على شدة المجال المغناطيسي (H) Magnetic Field Intensity

العلاقة التي تربط بينهما هي

B = m₀ H      (1)

حيث   m₀ معامل نفاذية الفراغ  (Permeability)

 كثافة  خطوط التأثير المغناطيسي  تكون دلالة على شدة المجال المغناطيسي

الفيض المغناطيسي F     Magnetic Flux

عندما يكون الحث المغناطيسي B منتظم  وعمودي على سطح منتظم مساحته  S  فان:

عدد خطوط الفيض التى تنفذ عموديا خلال  هذا السطح  تعرف بالفيض المغنطيسى F    ويعطى بـ :
  F = B S         (Wb/m²)  or Tesla                            (2)

j  تعرف بالفيض المغناطيسى  (Magnetic Flux) والذى يعرف بعدد خطوط الفيض التى تنفذ عموديا خلال سطح ما مساحتة S

ووحدات قياس B هى     تسلا =    Wb/m²

وإذا كان العمودي على السطح يصنع زاوية مقدارها q مع اتجاه خطوط القوى فإن المعادلة 2 تصبح على الشكل التالي

F  = B S   Cos q                              (3)

      فإذا كان السطح غير منتظم الشكل فيمكن تقسيمه إلى أسطح صغيرة مساحة كل سطح  Ds والمعادلة 2 تصبح

F = B cosq Ds                            (4)

F = B   cosq    ds                            (5)

أى أن السطح قسم إلى عناصر صغيرة متناهية في الصغر ds  

شدة المجال المغناطيسى لمغناطيس دائم عند نقطة قريبة منه وتقع على امتداد محوره مثل النقطة b

كما هو موضح بالرسم النقطة (b ) تبعد مسافة (a ) عن منتصف المغناطيس 

الذي طوله (ℓ ) فتكون شدة المجال تعطى من العلاقة   

تسمى  P_m العزم المغناطيسي وهي تساوي ( P_m = m ℓ.  ) حيث m هي شدة المغناطيس  ووحداتة   A.m 

* ملاحظة :

استمر العلماء لسنوات طويلة يدرسون المجال المغناطيسي منفصل تماما عن المجال الكهربي حتى استطاع العالم اورستد (1820م) أن يؤكد العلاقة الوثيقة بين المجالين الكهربي والمغناطيسي عندما اكتشف انحراف إبرة مغناطيسية عندما تقترب من سلك يمر به تيار كهربائي.

* الخلاصة : المجال المغناطيسي يحدث نتيجة مرور التيار الكهربي

قانون بيوت وسافارت (The Biot-Savart law)

 بيوت وسافارت هما عالمان استطاعا استنتاج قانون يمكن بواسطته حساب المجال المغناطيسي لأى دائرة كهربية.

نتاج دراسة عملية للمجال المغناطيسي الناتج عن مرور تيار كهربي مار في سلك ويؤثر على إبرة مغناطيسية موضوعة بالجوار . قام العالمين بيوت وسافارت بعدة تجارب لايجاد العلاقة بين التيار المار في سلك والمجال المغناطيسي الناتج عنه عند اي نقطة في الفراغ.  وقد توصلوا إلى الحقائق العملية التالية:

أن متجه المجال المغناطيسي  dB لعنصر صغير من السلك طوله  dℓ  عند نقطة  P  في الفراغ  تكون دائما عمودية على كلاً من العنصر dℓ   ومتجه الإزاحة  r        الذي يتجه من عنصر السلك dℓ  إلى النقطة P.

·         يتناسب مقدار المجال المغناطيسي dB  طرديا مع مقدار التيار المار في السلك.

·         يتناسب مقدار المجال المغناطيسي dB  طرديا مع sinq  حيث أن الزاويةq  هي الزاوية المحصورة بين متجه الإزاحة r  والعنصر من السلك dℓ  .

·         ويتناسب مقدار المجال المغناطيسي  dB  عكسيا مع مربع المسافة      r²  .

استنتاج القانون

عند مرور تيار كهربي (I) في سلك لإيجاد الحث المغناطيسي (dB)  لعنصر منه طوله ( dℓ)  كما بالرسم نلاحظ أن  

ومنها يكون

حيث (K_m) ثابت التناسب ساوي: 

وهذه المعادلة استنتجت من خلال التجارب والقياسات المعملية

ويكون الشكل النهائي للقانون هو:

الموضوع منقول من محاضرة للدكتور / محمد المرسي
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ

✓✓👈 روابط كتب أخرى مهمة :

👍》جميع كتب فيزياء pdf

👍》كتب فيزياء مترجمة pdf

👍》كتب إلكترونيات pdf

👍》كتب فيزياء إلكترونيات للمبتدئين pdf

👍》كتب أساسيات الكهرباء والإلكترونيات pdf

تعديل المقال